MỘT SỐ BÀI TOÁN CHỨNG MINH BẤT ĐẲNG THỨC (CƠ BẢN) |
Nhắc lại:
* BĐT Côsi áp dụng cho hai số không âm:
(1)
- Cách viết tương đương:. (2)
Dấuxẩy ra khi và chỉ khi
.
* Chú ý: Với hai số thực tùy ý, ta có:
-(Vì
.
* Một số kết quả thường dùng:
.
Thật vậy, vì 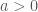 nên
nên  . Áp dụng BĐT (2) cho hai số này ta được:
. Áp dụng BĐT (2) cho hai số này ta được:
 .
.
.
Thật vậy, vì 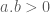 nên
nên  . Áp dụng BĐT (2) cho hai số này ta được:
. Áp dụng BĐT (2) cho hai số này ta được:
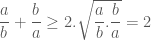 .
.
————————————
MỘT SỐ BÀI TẬP
Bài 1: Bài toán thuận.
Chứng minh rằng với mọita có:
.
Dấu đẳng thức (dấu bằng) xảy ra khi nào ?
Hướng dẫn:
Trong bài toán này có chứa hai số hạng dạng nghịc đảo. Vì đã có số hạng nên phần còn lại phải biểu diễn thành thừa số của
nên phần còn lại phải biểu diễn thành thừa số của 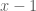 . Vậy ta phải viết lại vế trái như sau:
. Vậy ta phải viết lại vế trái như sau:
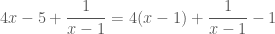 (*)
(*)
Vì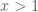 nên
nên  .
.
Áp dụng bất đẳng thức Côsi (2) cho 2 số dương , ta có:
, ta có:

Hay . (**)
. (**)
Kết hợp với (*), suy ra:
 .
.
Vậy (đpcm)
(đpcm)
Theo (**), dấu đẳng thức xảy ra

 (do
(do  )
)
 .
.
——-
Trong bài toán này có chứa hai số hạng dạng nghịc đảo. Vì đã có số hạng
Vì
Áp dụng bất đẳng thức Côsi (2) cho 2 số dương
Hay
Kết hợp với (*), suy ra:
Vậy
Theo (**), dấu đẳng thức xảy ra
——-
Bài 2: Bài toán ngược của dạng Bài toán 1.
Chứng minh rằng
Hướng dẫn:
Khác với bài 1, vế trái bài này có dạng tích, nên ta cần chú ý một dạng tương đường của BĐT (1) là . (3)
. (3)
Quay lại bài tập này, với mọi![x\in [1; 5] x\in [1; 5]](http://s0.wp.com/latex.php?latex=x%5Cin+%5B1%3B+5%5D&bg=ffffff&fg=4e4e4e&s=0) thì
thì 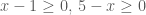 . Vậy áp dụng BĐT (3) cho hai số không âm này ta có:
. Vậy áp dụng BĐT (3) cho hai số không âm này ta có:
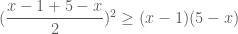
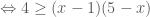 . (đpcm)
. (đpcm)
Dấu “=” xảy ra .
.
Khác với bài 1, vế trái bài này có dạng tích, nên ta cần chú ý một dạng tương đường của BĐT (1) là
Quay lại bài tập này, với mọi
Dấu “=” xảy ra
——————
BÀI TẬP TỰ GIẢI.
Chứng minh rằng:
1..
2.
3. Với mọi góc, ta có:
.
4..
5..
—————












.jpg)

![Ảnh bìa Facebook Timeline đẹp nhất [P2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiErai1d3SbxIXpZmLVa_Abc1NpkhhVamYwCM4_R6EHETUl4Kh7vkj-9lgKm5h2-zzTEMWuLtneTEaAfrBYqRl6y48k3GrDSiop3gS-WzgR-6Ba6C-H1cI8ILft9lJXjz8mbJ84S8ebnts/s72-c/anh_bia_facebook_kenhdaihoc.com_+(1).jpg)
![Ảnh bìa Facebook Timeline đẹp nhất [P3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhk7EG1TIxlQJctZKcpohjBAwzIcfWDo4Jxg6X5DRAk8Ay3dIMI3tC_cvNUYd2-N4ePZzwRTkhkVDHpqlUuKGg991WQhb-eB-JhQGHR9ykJimWATHoujI_8ihMpVh7kdOdDrmbukIsSwJw/s72-c/anh-bia_facebook_kenhdaihoc.com_dep+(1).jpg)
![Ảnh bìa Facebook Timeline đẹp nhất [P4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhS8ADsEtX4FJeXVlCRlZ7iwzWshDFIudf2Mhvo4kDwyOlmse-R1tARAQbs6ZhsHzcThgZF0jm1h72isInAJU1naU8EzGYD10EFDANjy47pG4ptuI__tQ6MrGUmZW251zr8dSZhEhtwJ4s/s72-c/anh_bia_facebook_kenhdaihoc.com_hot+(1).jpg)
.jpg)

.jpg)
0 nhận xét