A. Tìm giá trị lớn nhất,nhỏ nhất của hàm số
Bài toán 1: Tìm giá trị lớn nhất , nhỏ nhất của hàm số trên miền các định hay một khoảng. Phương pháp: - Tìm tập xác định
- Tính
 - Giải phương trình
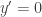 (các điểm tới hạn ) và tính giá trị tại các điểm tới hạn . (các điểm tới hạn ) và tính giá trị tại các điểm tới hạn . - Lập bảng biến thiên , căn cứ bảng biến thiên
 GTLN,GTNN. GTLN,GTNN.
Bài toán 2: Tìm GTLN,GTNN của hàm số trên một đoạn ![[a,b] [a,b]](http://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=333333&s=0) ? ? Phương pháp: - Tính
 - Giải phương trình
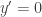 , để tìm các nghiệm , để tìm các nghiệm ![{x_1;x_2;...;x_n}\in[a;b] {x_1;x_2;...;x_n}\in[a;b]](http://s0.wp.com/latex.php?latex=%7Bx_1%3Bx_2%3B...%3Bx_n%7D%5Cin%5Ba%3Bb%5D&bg=ffffff&fg=333333&s=0) - Tính các giá trị
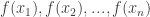 và và 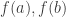 - GTLN là số lớn nhất trong các giá trị vừa tìm
- GTNN là số bé nhất trong các giá trị vừa tìm.
Ví dụ: a) Tìm giá trị lớn nhất , giá tẹi nhỏ nhất của hàm số: 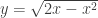
b) Tìm giá trị lớn nhất , giá tẹi nhỏ nhất của hàm số: 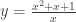 trên đoạn trên đoạn![\left[{\frac{1}{2};2}\right] \left[{\frac{1}{2};2}\right]](http://s0.wp.com/latex.php?latex=%5Cleft%5B%7B%5Cfrac%7B1%7D%7B2%7D%3B2%7D%5Cright%5D&bg=ffffff&fg=333333&s=0) Hướng dẩn giải: a) - Tập xác định : D=[0;2]
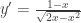 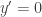 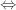 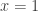  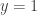 - Bảng biến thiên:( các em tự lập)
- Kết luận:
b) Bài tập rèn luyện: Bài 1: Tìm GTLN,GTNN của hàm số a) 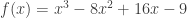 trên đoạn trên đoạn ![[1;3] [1;3]](http://s0.wp.com/latex.php?latex=%5B1%3B3%5D&bg=ffffff&fg=333333&s=0) . . b) 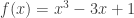 trên đoạn trên đoạn ![[0;2] [0;2]](http://s0.wp.com/latex.php?latex=%5B0%3B2%5D&bg=ffffff&fg=333333&s=0) . . c) 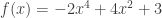 trên đoạn trên đoạn ![[0;2] [0;2]](http://s0.wp.com/latex.php?latex=%5B0%3B2%5D&bg=ffffff&fg=333333&s=0) . . Bài 2: Tìm GTLN,GTNN của hàm số a) 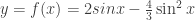 trên đoạn trên đoạn ![[0;\pi] [0;\pi]](http://s0.wp.com/latex.php?latex=%5B0%3B%5Cpi%5D&bg=ffffff&fg=333333&s=0) . . b) 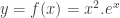 trên đoạn trên đoạn ![[-3;2] [-3;2]](http://s0.wp.com/latex.php?latex=%5B-3%3B2%5D&bg=ffffff&fg=333333&s=0) . . c)  d) 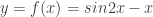 trên đoạn trên đoạn ![\left[ {-\frac{\pi }{2};\frac{\pi }{2}} \right] \left[ {-\frac{\pi }{2};\frac{\pi }{2}} \right]](http://s0.wp.com/latex.php?latex=%5Cleft%5B+%7B-%5Cfrac%7B%5Cpi+%7D%7B2%7D%3B%5Cfrac%7B%5Cpi+%7D%7B2%7D%7D+%5Cright%5D&bg=ffffff&fg=333333&s=0) . . Bài 3: Tìm GTLN,GTNN của hàm số a) 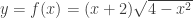 b) 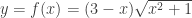 c) 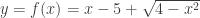
B. Tìm điều kiện để hàm số y = f(x,m) có GTLN (GTNN) trên đoạn [a; b] là một số cho trước
Phương pháp giải:Giả sử bài toán yêu cầu: Tìm giá trị của tham số 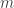 để hàm số để hàm số 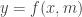 có giá trị lớn nhất (giá trị nhỏ nhất ) trên đoạn có giá trị lớn nhất (giá trị nhỏ nhất ) trên đoạn ![[a;b] [a;b]](http://s0.wp.com/latex.php?latex=%5Ba%3Bb%5D&bg=ffffff&fg=333333&s=0) là là 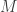 (là m), ta có thể tiến hành theo một tring các cách sau. (là m), ta có thể tiến hành theo một tring các cách sau. Chú ý: Hàm số 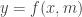 liên tục trên liên tục trên ![[a;b] [a;b]](http://s0.wp.com/latex.php?latex=%5Ba%3Bb%5D&bg=ffffff&fg=333333&s=0) Cách 1: - Tính đạo hàm
 - Gải phương trình
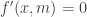 để tìm các nghiệm để tìm các nghiệm ![{x_1;x_2;...;x_n}\in[a;b] {x_1;x_2;...;x_n}\in[a;b]](http://s0.wp.com/latex.php?latex=%7Bx_1%3Bx_2%3B...%3Bx_n%7D%5Cin%5Ba%3Bb%5D&bg=ffffff&fg=333333&s=0) - Tính các giá trị
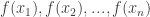 và và 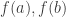 - Từ các kết quả trên, xác định GTLN (GTNN) của hàm số , giả sử là
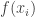 - Giải phương trình
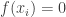 để tìm nghiệm để tìm nghiệm 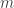 - Nêu kết luận cho bài toán để hoàn tất bài toán.
Cách 2: - Xác định điều kiện để bất phương trình :
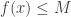 được thỏa mãn được thỏa mãn ![\forall x \in [a;b] \forall x \in [a;b]](http://s0.wp.com/latex.php?latex=%5Cforall+x+%5Cin+%5Ba%3Bb%5D&bg=ffffff&fg=333333&s=0) - Giải điều kiện vừa tìm để xác định các giá trị của
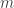 thỏa điều kiện vừa nêu thỏa điều kiện vừa nêu - Xác định điều kiện để phương trình:
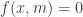 có nghiệm có nghiệm ![x\in [a; b] x\in [a; b]](http://s0.wp.com/latex.php?latex=x%5Cin+%5Ba%3B+b%5D&bg=ffffff&fg=333333&s=0) - Giải điều kiện vừa tìm để xác định các giá trị của
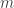 thỏa điều kiện thỏa điều kiện - So sánh các giá trị của m tìm được ở các bước 2 và 3 để chọn ra giá trị m thỏa bài toán
- Nêu kết luận cho bài toán để hoàn tất bài toán.
Cách 3: - Tính đạo hàm
 - Giải phương trình
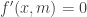 để tìm các nghiệm để tìm các nghiệm ![{x_1;x_2;...;x_n}\in[a;b] {x_1;x_2;...;x_n}\in[a;b]](http://s0.wp.com/latex.php?latex=%7Bx_1%3Bx_2%3B...%3Bx_n%7D%5Cin%5Ba%3Bb%5D&bg=ffffff&fg=333333&s=0) - Tính các giá trị
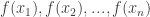 và và 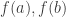 - Lần lượt giải các phương trình:
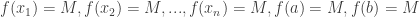 để tìm các nghiệm để tìm các nghiệm 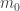 của chúng của chúng - Thay
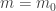 vào hàm số và kiểm tra trực tiếp xem giá trị vào hàm số và kiểm tra trực tiếp xem giá trị 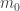 thực sự thỏa bài toán để nhận hoặc loại giá trị thực sự thỏa bài toán để nhận hoặc loại giá trị 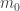 - Nêu kết luận cho bài toán để hoàn tất bài toán.
Bài tập 1: Xét hàm số: 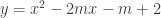 . Xác định giá trị của tham số $latex m$ sao cho hàm số giá trịlớn nhất trên . Xác định giá trị của tham số $latex m$ sao cho hàm số giá trịlớn nhất trên ![[1; 3] [1; 3]](http://s0.wp.com/latex.php?latex=%5B1%3B+3%5D&bg=ffffff&fg=333333&s=0) là là 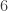 Hướng dẩn giải: - Ta có đạo hàm
 : : 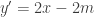 , vậy , vậy 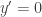 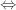 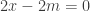 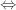 x=m x=m - Nhận xét rằng :
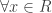 , , 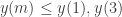
- Do vậy hàm số đạt giá trị lớn nhất trên
![[1;3] [1;3]](http://s0.wp.com/latex.php?latex=%5B1%3B3%5D&bg=ffffff&fg=333333&s=0) hoặc tại hoặc tại 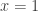 hoặc tại hoặc tại 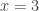 , suy ra , suy ra
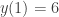 (1) (1)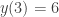 (2) (2)
- Do
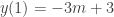 , nên từ (1) suy ra , nên từ (1) suy ra 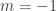 - Do
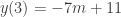 , nên từ (2) suy ra , nên từ (2) suy ra 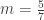
Với 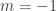 , thay vào hàm số ta được: , thay vào hàm số ta được: 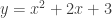 . . Bảng biến thiên: (các em tự lập) Vậy giá trị lớn nhất của hàm số trên ![[1;3] [1;3]](http://s0.wp.com/latex.php?latex=%5B1%3B3%5D&bg=ffffff&fg=333333&s=0) là là 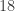 , suy ra , suy ra 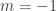 không thỏa bài toán không thỏa bài toán Suy ra 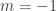 loại loại Với 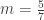 , thay vào hàm số ta được : , thay vào hàm số ta được : 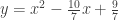 Bảng biến thiên: (các em tự lập) Vậy giá trị lớn nhất của hàm số trên ![[1;3] [1;3]](http://s0.wp.com/latex.php?latex=%5B1%3B3%5D&bg=ffffff&fg=333333&s=0) là là 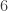 Suy ra giá trị 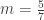 thỏa mãn bài toán . thỏa mãn bài toán . - Kết luận: Giá trị cần tìm :
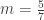
|












.jpg)

![Ảnh bìa Facebook Timeline đẹp nhất [P2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiErai1d3SbxIXpZmLVa_Abc1NpkhhVamYwCM4_R6EHETUl4Kh7vkj-9lgKm5h2-zzTEMWuLtneTEaAfrBYqRl6y48k3GrDSiop3gS-WzgR-6Ba6C-H1cI8ILft9lJXjz8mbJ84S8ebnts/s72-c/anh_bia_facebook_kenhdaihoc.com_+(1).jpg)
![Ảnh bìa Facebook Timeline đẹp nhất [P3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhk7EG1TIxlQJctZKcpohjBAwzIcfWDo4Jxg6X5DRAk8Ay3dIMI3tC_cvNUYd2-N4ePZzwRTkhkVDHpqlUuKGg991WQhb-eB-JhQGHR9ykJimWATHoujI_8ihMpVh7kdOdDrmbukIsSwJw/s72-c/anh-bia_facebook_kenhdaihoc.com_dep+(1).jpg)
![Ảnh bìa Facebook Timeline đẹp nhất [P4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhS8ADsEtX4FJeXVlCRlZ7iwzWshDFIudf2Mhvo4kDwyOlmse-R1tARAQbs6ZhsHzcThgZF0jm1h72isInAJU1naU8EzGYD10EFDANjy47pG4ptuI__tQ6MrGUmZW251zr8dSZhEhtwJ4s/s72-c/anh_bia_facebook_kenhdaihoc.com_hot+(1).jpg)
.jpg)

.jpg)
0 nhận xét