Lí thuyết xác suất là ngành toán học chuyên nghiên cứu xác suất.
Các nhà toán học coi xác suất là các số trong khoảng
[0,1], được gán tương ứng với một biến cố mà khả năng xảy ra hoặc không xảy ra là ngẫu nhiên. Kí hiệu xác suất P(E) được gán cho biến cố E theo tiên đề xác suất.Xác suất mà biến cố E xảy ra khi biết việc xảy ra của biến cố F là một xác suất có điều kiện của E khi biết F; giá trị số của nó là  (với điều kiện là P(F) khác 0). Nếu xác suất có điều kiện của E khi biết F là bằng với xác suất ("không có điều kiện")của E, thì E và F được xem là các sự kiện độc lập. Vì quan hệ giữa E và F là đối xứng nên ta có thể nói rằng
(với điều kiện là P(F) khác 0). Nếu xác suất có điều kiện của E khi biết F là bằng với xác suất ("không có điều kiện")của E, thì E và F được xem là các sự kiện độc lập. Vì quan hệ giữa E và F là đối xứng nên ta có thể nói rằng 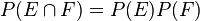 .
.
 (với điều kiện là P(F) khác 0). Nếu xác suất có điều kiện của E khi biết F là bằng với xác suất ("không có điều kiện")của E, thì E và F được xem là các sự kiện độc lập. Vì quan hệ giữa E và F là đối xứng nên ta có thể nói rằng
(với điều kiện là P(F) khác 0). Nếu xác suất có điều kiện của E khi biết F là bằng với xác suất ("không có điều kiện")của E, thì E và F được xem là các sự kiện độc lập. Vì quan hệ giữa E và F là đối xứng nên ta có thể nói rằng 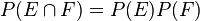 .
.Hai khái niệm chủ đạo trong lí thuyết xác suất là biến ngẫu nhiên và phân bố xác suất của một biến ngẫu nhiên; xem thông tin cụ thể ở các bài tương ứng.
Một cái nhìn trừu tượng về xác suất
Các nhà toán học "thuần túy" thường xem lí thuyết xác suất là ngành nghiên cứu về các biến ngẫu nhiên và không gian xác suất — hướng này được đưa ra bởi Kolmogorov vào thập niên 1930. Một không gian xác suất là một bộ ba  , trong đó:
, trong đó:
 , trong đó:
, trong đó:- Ω là tập không rỗng, đôi khi gọi là "không gian mẫu", trong đó mỗi thành viên của nó được coi là một kết quả có thể xảy ra của một thực nghiệm ngẫu nhiên. Ví dụ, nếu chọn ngẫu nhiên 100 cử tri trong số các cử tri tại California và hỏi họ sẽ bầu cho ai vào chức vụ thống đốc, thì tập tất cả các dãy gồm 100 cử tri California sẽ là không gian mẫu Ω.
 là một σ-đại số của các tập con của Ω, các thành viên của nó được gọi là các "biến cố". Ví dụ, tập tất cả các chuỗi gồm 100 cử tri California trong đó ít nhất 60 người sẽ bầu cho Schwarzenegger được xem là "biến cố" rằng ít nhất 60 trong số 100 người được chọn sẽ bầu cho Schwarzenegger. Nói rằng
là một σ-đại số của các tập con của Ω, các thành viên của nó được gọi là các "biến cố". Ví dụ, tập tất cả các chuỗi gồm 100 cử tri California trong đó ít nhất 60 người sẽ bầu cho Schwarzenegger được xem là "biến cố" rằng ít nhất 60 trong số 100 người được chọn sẽ bầu cho Schwarzenegger. Nói rằng  là một σ-đại số có nghĩa rằng, theo định nghĩa, nó chứa Ω, rằng phần bù của một biến cố bất kì là một biến cố, và rằng hợp của một chuỗi (hữu hạn hay vô hạn đếm được) các biến cố bất kì là một biến cố.
là một σ-đại số có nghĩa rằng, theo định nghĩa, nó chứa Ω, rằng phần bù của một biến cố bất kì là một biến cố, và rằng hợp của một chuỗi (hữu hạn hay vô hạn đếm được) các biến cố bất kì là một biến cố.
- P là một độ đo (cụ thể là độ đo xác suất) trên
 , sao cho P(Ω) = 1,.
, sao cho P(Ω) = 1,.
Cần chú ý rằng P là hàm xác định trên  chứ không phải trên Ω.
chứ không phải trên Ω.
 chứ không phải trên Ω.
chứ không phải trên Ω.Với Ω đếm được, ta có thể định nghĩa  là tập lũy thừa (powerset) của Ω, nghĩa là
là tập lũy thừa (powerset) của Ω, nghĩa là  , đó là một σ-đại số và là đại số lớn nhất mà ta có thể tạo được bằng Ω. Do đó, trong một không gian rời rạc, ta có thể bỏ qua F và chỉ viết (Ω,P) khi định nghĩa nó.
, đó là một σ-đại số và là đại số lớn nhất mà ta có thể tạo được bằng Ω. Do đó, trong một không gian rời rạc, ta có thể bỏ qua F và chỉ viết (Ω,P) khi định nghĩa nó.
 là tập lũy thừa (powerset) của Ω, nghĩa là
là tập lũy thừa (powerset) của Ω, nghĩa là  , đó là một σ-đại số và là đại số lớn nhất mà ta có thể tạo được bằng Ω. Do đó, trong một không gian rời rạc, ta có thể bỏ qua F và chỉ viết (Ω,P) khi định nghĩa nó.
, đó là một σ-đại số và là đại số lớn nhất mà ta có thể tạo được bằng Ω. Do đó, trong một không gian rời rạc, ta có thể bỏ qua F và chỉ viết (Ω,P) khi định nghĩa nó.Mặt khác, nếu Ω không đếm được và ta dùng  , ta sẽ gặp rắc rối khi định nghĩa phép đo xác suất P vì F quá lớn, nghĩa là sẽ có các tập mà không thể gán cho nó một độ đo duy nhất, ví dụ Banach-Tarski Paradox. Do đó, ta phải dùng một σ-đại số
, ta sẽ gặp rắc rối khi định nghĩa phép đo xác suất P vì F quá lớn, nghĩa là sẽ có các tập mà không thể gán cho nó một độ đo duy nhất, ví dụ Banach-Tarski Paradox. Do đó, ta phải dùng một σ-đại số  nhỏ hơn (ví dụ. đại số Borel của Ω là σ-đại số nhỏ nhất có thể làm cho tất cả các tập mở trở nên đo được).
nhỏ hơn (ví dụ. đại số Borel của Ω là σ-đại số nhỏ nhất có thể làm cho tất cả các tập mở trở nên đo được).
 , ta sẽ gặp rắc rối khi định nghĩa phép đo xác suất P vì F quá lớn, nghĩa là sẽ có các tập mà không thể gán cho nó một độ đo duy nhất, ví dụ Banach-Tarski Paradox. Do đó, ta phải dùng một σ-đại số
, ta sẽ gặp rắc rối khi định nghĩa phép đo xác suất P vì F quá lớn, nghĩa là sẽ có các tập mà không thể gán cho nó một độ đo duy nhất, ví dụ Banach-Tarski Paradox. Do đó, ta phải dùng một σ-đại số  nhỏ hơn (ví dụ. đại số Borel của Ω là σ-đại số nhỏ nhất có thể làm cho tất cả các tập mở trở nên đo được).
nhỏ hơn (ví dụ. đại số Borel của Ω là σ-đại số nhỏ nhất có thể làm cho tất cả các tập mở trở nên đo được).Một biến ngẫu nhiên X là một measurable function (hàm đo được) trên Ω. Ví dụ, số cử tri sẽ bầu cho Schwarzenegger trong mẫu 100 người là một biến ngẫu nhiên.
Nếu X là biến ngẫu nhiên bất kì, kí hiệu  , viết tắt của
, viết tắt của  , là xác suất của "biến cố"
, là xác suất của "biến cố"  .
.
 , viết tắt của
, viết tắt của  , là xác suất của "biến cố"
, là xác suất của "biến cố"  .
.Về các phương pháp đại số khác với cách tiếp cận của Kolmogorov, mời xem bài algebra of random variables.
Triết lí trong ứng dụng của xác suất
Một số nhà thống kê chỉ gán các xác suất cho các biến cố ngẫu nhiên, ví dụ, các biến ngẫu nhiên, mà cho kết quả thử nghiệm thực hay mang tính lí thuyết; đó là những nhà tần suất học (frequentist).
Một số khác lại gán xác suất với những mệnh đề không chắc chắn, tùy theo mức độ chủ quan (personal probability) tin vào sự đúng đắn của nó. Những người như vậy là các nhà Bayes. Một nhà Bayes có thể gán một xác suất cho một mệnh đề như 'đã từng có sự sống trên Sao Hỏa một tỉ năm trước,' vì điều đó là không chắc chắn, trong khi một nhà tần suất học sẽ không gán xác suất cho những phát biểu ngẫu nhiên như vậy. Một nhà tấn suất học có thể xem lời tuyên bố đó là không có ý nghĩa. Các nhà tần suất học chỉ gán xác suất cho kết quả của những thử nghiệm ngẫu nhiên được định nghĩa tốt, nghĩa là, khi có một không gian mẫu định sẵn. Trong kinh tế, xác suất đóng góp rất nhiều cho việc tính toán và đưa ra các giải pháp nghiên cứu thị trường,...
Một số khác lại gán xác suất với những mệnh đề không chắc chắn, tùy theo mức độ chủ quan (personal probability) tin vào sự đúng đắn của nó. Những người như vậy là các nhà Bayes. Một nhà Bayes có thể gán một xác suất cho một mệnh đề như 'đã từng có sự sống trên Sao Hỏa một tỉ năm trước,' vì điều đó là không chắc chắn, trong khi một nhà tần suất học sẽ không gán xác suất cho những phát biểu ngẫu nhiên như vậy. Một nhà tấn suất học có thể xem lời tuyên bố đó là không có ý nghĩa. Các nhà tần suất học chỉ gán xác suất cho kết quả của những thử nghiệm ngẫu nhiên được định nghĩa tốt, nghĩa là, khi có một không gian mẫu định sẵn. Trong kinh tế, xác suất đóng góp rất nhiều cho việc tính toán và đưa ra các giải pháp nghiên cứu thị trường,...
Không gian mẫu
Trong lý thuyết xác suất, không gian mẫu hay không gian mẫu toàn thể, thường được kí hiệu là S, Ω hay U (tức "universe"), của một thí nghiệm hay của một phép thử ngẫu nhiên là tập hợp của tất cả các kết quả có thể xảy ra. Ví dụ, trong thí nghiệm tung một đồng xu, không gian mẫu của thí nghiệm đó là tập hợp {ngửa, sấp}. Còn đối với thí nghiệm tung một con xúc xắc có sáu mặt thì, không gian mẫu là tập {1, 2, 3, 4, 5, 6}. Bất kì tập hợp con nào của không gian mẫu đều thường được gọi là một biến cố, khi tập con của không gian mẫu chỉ chứa một phần tử thì được gọi là biến cố cơ bản. Mỗi phần tử của không gian mẫu được gọi là một mẫu.
Đối với một số thí nghiệm, có thể có hai hoặc nhiều hơn không gian mẫu. Ví dụ, khi rút một quân bài từ một bộ bài thường, có 52 cây, một khả năng cho không gian mẫu có thể là hạng của quân bài (từ quân Xì tới quân Già), trong khi khả năng kia có thể là hoa của quân bài (chuồn, rô, cơ, bích). Một sự thể hiện hoàn chỉnh về kết quả, tuy nhiên, phải xác định được cả thứ hạng và hoa của lá bài, và một không gian mẫu mô tả cụ thể từng lá bài có thể được xây dựng bằng tích Descartes của hai không gian đã nêu trên.
Không gian mẫu có vẻ như là một cách tiếp cận xác suất rất tự nhiên (tức là ngay từ khi nghiên cứu xác suất người ta đã đưa ra khái niệm này rồi), nhưng nó là thành phần quan trọng trong không gian xác suất (một khái niệm của xác suất hiện đại). Một không gian xác suất (Ω, F, P) kết hợp chặt chẽ giữa một không gian mẫu kết quả, Ω, định nghĩa cho một tập biến cố theo sở thích, σ-đại số F, mà theo đó, đơn vị đo xác suất P được định nghĩa.
Biến ngẫu nhiên
Biến ngẫu nhiên là một thuật ngữ được dùng trong toán học và thống kê. Trong một phép thử ngẫu nhiên (random experiment), đầu ra (outcome) của nó có thể là giá trị số hoặc không phải. Ví dụ phép thử ngẫu nhiên là tung một đồng xu lên và xét mặt nào của đồng xu ở phía trên, thì kết quả đầu ra có thể là {sấp, ngửa} (đầu ra không phải là số). Ví dụ phép thử ngẫu nhiên là tung con súc sắc và xem mặt nằm phía trên là có mấy chấm, thì kết quả đầu ra có thể là {1,2,3,4,5,6} (đầu ra là số). Tuy nhiên, trong các ứng dụng của thống kê, người ta muốn mỗi đầu ra đều gắn với một đại lượng đo đạc được, hay còn gọi là thuộc tính có giá trị là số. Để thực hiện điều này, người ta định ra biến ngẫu nhiên để ánh xạ mỗi đầu ra của một phép thử ngẫu nhiên với một giá trị số.
Biến ngẫu nhiên là một hàm toán học với đặc điểm: nó gán một giá trị bằng số cho kết quả (đầu ra) của một phép thử ngẫu nhiên (thực nghiệm).
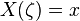
với ζ là đại diện cho đầu ra của một thực nghiệm, x là một số thực, X là hàm ánh xạ (hay là biến ngẫu nhiên). Vì thế, người ta còn gọi X là biến ngẫu nhiên giá trị thực (real-valued random variable).
Ví dụ: trong phép thử ngẫu nhiên tung đồng xu, ta định ra một biến ngẫu nhiên tương ứng

Ví dụ: trong phép thử ngẫu nhiên tung con xúc xắc, vì đầu ra vốn dĩ đã là số thực, nên ta có thể ánh xạ trực tiếp đầu ra bằng hàm đồng nhất thức

Phép thử ngẫu nhiên trong trường hợp tung con xúc xắc còn được gọi là phép thử ngẫu nhiên có giá trị bằng số (numerically valued random experiment).
Thuật ngữ biến trong biến ngẫu nhiên không có nghĩa nó là một biến như các biến toán học khác, mà thực chất nó là một hàm số (hay ánh xạ). Ta không thể gán giá trị cụ thể cho một biến ngẫu nhiên; một biến ngẫu nhiên không mô tả kết quả thực tế của một thực nghiệm cụ thể, nó dùng các số thực để mô tả các kết quả có thể có nhưng chưa xác định.
Thuật ngữ ngẫu nhiên trong biến ngẫu nhiên không có nghĩa nó là một hàm số ngẫu nhiên, mà nó là một hàm số được xác định. Tính ngẫu nhiên được thể hiện ở tham số đầu vào ζ. Điều này dẫn tới đầu ra của hàm (hay biến ngẫu nhiên) là ngẫu nhiên. Nói tóm lại, biến ngẫu nhiên có thể được xem là kết quả bằng số của việc vận hành một cơ chế không đơn định hoặc thực hiện một thực nghiệm không đơn định để tạo ra một kết quả ngẫu nhiên. Ví dụ, một biến ngẫu nhiên có thể mô tả các kết quả có thể của việc chọn ngẫu nhiên một người và đo chiều cao của người đó.
Tuy các ví dụ đơn giản như thả súc sắc và đo chiều cao (như miêu tả ở trên) giúp ta dễ dàng hình dung về ứng dụng thực tế của các biến ngẫu nhiên, cấu trúc toán học của chúng mang lại cho các nhà toán học sự thuận tiện khi làm việc với lý thuyết xác suất độ đo trong một môi trường quen thuộc hơn với các hàm số giá trị thực. Ngược lại, khái niệm này cũng đặt các thực nghiệm có liên quan đến các kết quả với giá trị là số thực vào trong khuôn khổ lý thuyết độ đo một cách vững chắc.
Biến cố (lí thuyết xác suất)
Trong lí thuyết xác suất, một biến cố (event) là một tập các kết quả đầu ra (outcomes) (hay còn gọi là một tập con của không gian mẫu) mà tương ứng với nó người ta sẽ gán kèm với một số thực (hay còn gọi là một xác suất). Thông thường, nếu không gian mẫu là hữu hạn, thì bất kì tập con nào của không gian mẫu cũng được xem là một biến cố. Tuy nhiên, điều này không đúng trong trường hợp không gian mẫu là vô hạn, đáng chú ý là khi đầu ra của một phép thử (experiment) là một số thực. Vì thế, khi định ra một không gian xác suất, nếu có thể, người ta thường tìm cách loại bỏ các tập con của không gian mẫu mà không được xem là biến cố.
Ví dụ
Nếu ta dùng một bộ bài gồm có 52 lá, và thực hiện việc rút ra một lá từ bộ bài, như vậy có tất cả 52 khả năng đầu ra hay ta nói không gian mẫu là tập hợp 52 phần tử. Một biến cố, là một tập con của không gian mẫu, kể cả tập cơ sở (chỉ chứa 1 phần tử) và cả không gian mẫu. Như vậy, ta có một vài biến cố:

Tính theo tỉ lệ diện tích, xác suất của A xấp xỉ bằng 0.4.
- "Rút ra lá bài vừa đỏ vừa đen cùng một lúc" (0 phần tử),
- "Lá bài rút ra là con 5 cơ" (1 phần tử),
- "Lá bài rút ra là con Già" (4 phần tử),
- "Lá bài rút ra là một lá bài" (52 phần tử).
Vì mọi biến cố đều là các tập hợp, chúng thường được biễu diễn dưới dạng liệt kê (ví dụ: {1, 2, 3}), và dùng sơ đồ Venn để minh họa.
Biến cố trong không gian xác suất
Việc liệt kê các tập con của không gian mẫu chỉ phù hợp khi số đầu ra là hữu hạn. Trong nhiều phân bố xác suất chuẩn, ví dụ phân bố chuẩn, thì không gian mẫu là tập con của tập các số thực. Nên việc qui định xác suất tương ứng cho mọi tập con của tập số thực là không khả thi. Vì thế, việc giới hạn sự tập trung vào một số biến cố nhất định là cần thiết.
Trong mô tả của lí thuyết ước lượng chung của không gian xác suất, một biến cố có thể được định nghĩa là một phần tử của một σ-đại số được chọn ra của các tập con của không gian mẫu. Dưới quan điệm này, tập con nào của không gian mẫu mà không phải là một phần tử của σ-đại số thì không được coi là một biến cố, và hiển nhiên là sẽ không có xác suất tương ứng.
Qui ước kí hiệu
Mặc dù các biến cố là các tập con của một không gian mẫu Ω, chúng thường được viết dưới dạng công thức mệnh đề (propositional formula) có chứa các biến ngẫu nhiên. Ví dụ, nếu X là một biến ngẫu nhiên giá trị thực được định nghĩa trên không gian mẫu Ω, thì biến cố
có thể được viết đơn giản là,
Cái này được dùng phổ biến trong các công thức xác suất, như
Giá trị kỳ vọng
- Trong Lý thuyết xác suất, giá trị kỳ vọng, giá trị mong đợi (hoặc kỳ vọng toán học), hoặc trung bình (mean) của một biến ngẫu nhiên là trung bình có trọng số của tất cả các giá trị của thể của biến đó, hay là được tính bằng tổng các tích giữa xác suất xảy ra của mỗi giá trị có thể của biến với giá trị đó. Như vậy, nó biểu diễn giá trị trung bình mà người ta "mong đợi" thắng cược nếu đặt cược liên tục nhiều lần với khả năng thắng cược là như nhau. Lưu ý rằng bản thân giá trị đó có thể không được mong đợi theo nghĩa thông thường; nó có thể ít có khả năng xảy ra hoặc không thể xảy ra. Một trò chơi hoặc một tình huống trong đó giá trị kỳ vọng bằng 0 được gọi là một "trò chơi công bằng" (fair game).
Ví dụ, một vòng quay roulette có 38 kết quả có thể có khả năng như nhau. Mỗi đặt cược vào một số duy nhất thắng 35-1 ( nghĩa là ta được trả 35 lần số tiền đặt cược và được nhận lại tiền đặt cược, vậy ta nhận được 36 lần tiền cược). Do đó, xét cả 38 kết quả có thể, giá trị kỳ vọng của khoản lợi thu được từ 1 đôla đặt cược cho một số duy nhất là:
nghĩa là khoảng -$0.0526. Do đó, giá trị kỳ vọng là ta sẽ mất trung bình hơn năm xu cho mỗi đôla tiền đặt cược.
Định nghĩa toán học
Thông thường, nếu  là một biến ngẫu nhiên xác định trên một không gian xác suất
là một biến ngẫu nhiên xác định trên một không gian xác suất  , thì giá trị kỳ vọng của
, thì giá trị kỳ vọng của  (ký hiệu
(ký hiệu  hoặc đôi khi
hoặc đôi khi  hoặc
hoặc 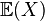 ) được định nghĩa như sau
) được định nghĩa như sau
 là một biến ngẫu nhiên xác định trên một không gian xác suất
là một biến ngẫu nhiên xác định trên một không gian xác suất  , thì giá trị kỳ vọng của
, thì giá trị kỳ vọng của  (ký hiệu
(ký hiệu  hoặc đôi khi
hoặc đôi khi  hoặc
hoặc 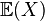 ) được định nghĩa như sau
) được định nghĩa như sautrong đó sử dụng tích phân Lebesgue. Lưu ý rằng không phải mọi biến ngẫu nhiên đều có một giá trị kỳ vọng, do có thể không tồn tại tích phân (ví dụ phân bố Cauchy). Hai biến ngẫu nhiên có cùng phân bố xác suất sẽ có giá trị kỳ vọng bằng nhau.
Nếu X là một biến ngẫu nhiên rời rạc với các giá trị x1, x2, ... và các xác suất tương ứng là p1, p2, ... với tổng bằng 1, thìE(X) có thể được tính bằng tổng của chuỗi
cũng như trong ví dụ đánh bạc nêu trên.
Nếu phân bố xác suất của X chấp nhận một hàm mật độ xác suất f(x), thì giá trị kỳ vọng có thể được tính như sau
Định nghĩa của trường hợp rời rạc trực tiếp suy ra rằng nếu X là một hằng biến ngẫu nhiên (constant random variable), nghĩa là X = b với một b là một số thực không đổi nào đó, thì giá trị kỳ vọng của X cũng bằng b.
Giá trị kỳ vọng của một hàm g(x) tùy ý của x, với hàm mật độ xác suất f(x) có công thức
Các tính chất
Tuyến tính
Phép toán giá trị kỳ vọng (hay phép toán kỳ vọng) E là phép toán tuyến tính theo nghĩa sau
với hai biến ngẫu nhiên X và Y bất kỳ (được định nghĩa trên cùng một không gian xác suất) và hai số thực bất kỳ a và b.
Kỳ vọng lặp
Với hai biến ngẫu nhiên bất kỳ X,Y, ta có thể định nghĩa kỳ vọng có điều kiện (conditional expectation):
Khi đó giá trị kỳ vọng của X thỏa mãn
Do đó, đẳng thức sau là đúng:
Vế phải của đẳng thức được gọi là kỳ vọng lặp. Mệnh đề này được nói đến trong quy tắc kỳ vọng toàn thể (law of total expectation)
Bất đẳng thức
Nếu một biến ngẫu nhiên X luôn nhỏ hơn hay bằng một biến ngẫu nhiên Y khác, kỳ vọng của X cũng nhỏ hơn hay bằng kỳ vọng của Y:
Nếu  , thì
, thì ![\mathrm{E}[X] \leq \mathrm{E}[Y]](http://upload.wikimedia.org/math/0/f/4/0f43294f17c1a65545d1a49278c0bf3d.png) .
.
 , thì
, thì ![\mathrm{E}[X] \leq \mathrm{E}[Y]](http://upload.wikimedia.org/math/0/f/4/0f43294f17c1a65545d1a49278c0bf3d.png) .
.Đặc biệt, do 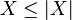 và
và  , giá trị tuyệt đối của kỳ vọng của một biến ngẫu nhiên nhỏ hơn hay bằng kỳ vọng của giá trị tuyệt đối của nó:
, giá trị tuyệt đối của kỳ vọng của một biến ngẫu nhiên nhỏ hơn hay bằng kỳ vọng của giá trị tuyệt đối của nó:
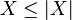 và
và  , giá trị tuyệt đối của kỳ vọng của một biến ngẫu nhiên nhỏ hơn hay bằng kỳ vọng của giá trị tuyệt đối của nó:
, giá trị tuyệt đối của kỳ vọng của một biến ngẫu nhiên nhỏ hơn hay bằng kỳ vọng của giá trị tuyệt đối của nó:Biểu diễn
Công thức sau đúng với mọi biến ngẫu nhiên giá trị thực không âm X (sao cho ![\mathrm{E}[X] < \infty](http://upload.wikimedia.org/math/6/2/a/62a5555ab26459825aa3912bae5c81b9.png) ), và số thực α lớn hơn 0:
), và số thực α lớn hơn 0:
![\mathrm{E}[X] < \infty](http://upload.wikimedia.org/math/6/2/a/62a5555ab26459825aa3912bae5c81b9.png) ), và số thực α lớn hơn 0:
), và số thực α lớn hơn 0:Không có tính nhân
Nói chung, phép toán giá trị kỳ vọng không có tính nhân, nghĩa là E(XY) không nhất thiết bằng E(X)E(Y), ngoại trừ nếu X vàY là độc lập hoặc không tương quan (uncorrelated). Sự không có tính nhân này dẫn đến nghiên cứu về hiệp phương sai (covariance) và sự tương quan (correlation).
Không bất biến về hàm
Nói chung, phép toán kỳ vọng và hàm của các biến ngẫu nhiên không có tính hoán vị; nghĩa là
trừ trường hợp được ghi chú như ở trên.
Ứng dụng của giá trị kỳ vọng
Các giá trị kỳ vọng của các lũy thừa của X được gọi là mômen (moment) của X; mômen quanh trung bình (moment about the mean) của X là các giá trị kỳ vọng của các lũy thừa của X − E(X). Mômen của một số biến ngẫu nhiên có thể được sử dụng để xác định phân bố của chúng, bằng các hàm sinh mômen (moment generating function) của chúng.
Để ước lượng bằng thực nghiệm giá trị kỳ vọng của một biến ngẫu nhiên, người ta liên tục thực hiện các quan sát về biến đó và tính trung bình cộng của các kết quả. Quy trình này ước lượng giá trị kỳ vọng thực sự bằng một cách không thiên lệch và có tính chất cực tiểu hóa tổng bình phương của các thặng dư (tổng bình phương của các hiệu giữa các quan sát và ước lượng). Luật số lớn chứng minh rằng (trong điều kiện ôn hòa) khi kích thước của mẫu thống kê lớn lên thì phương sai của ước lượng này sẽ nhỏ đi.
Trong Cơ học cổ điển, tâm khối (center of mass) là khái niệm tương đương với giá trị kỳ vọng. Ví dụ, giả sử X là một biến ngẫu nhiên rời rạc với các giá trị xi và các xác suất tương ứng pi. Xét một thanh ngang có trọng lượng không đáng kể, trên đó đặt các quả cân, tại các vị trí xi là các khối lượng pi (với tổng bằng 1). Điểm mà tại đó thanh ngang được thăng bằng (trọng tâm của nó) là E(X). (Tuy nhiên, cần lưu ý rằng tâm khối không đồng nghĩa với trọng tâm (center of gravity).)
Kỳ vọng của ma trận
Nếu X là một ma trận  , giá trị kỳ vọng của X là một ma trận của các giá trị kỳ vọng:
, giá trị kỳ vọng của X là một ma trận của các giá trị kỳ vọng:
 , giá trị kỳ vọng của X là một ma trận của các giá trị kỳ vọng:
, giá trị kỳ vọng của X là một ma trận của các giá trị kỳ vọng:Tính chất này được dùng trong các ma trận hiệp phương sai (covariance matrix).










 = \mathrm{E}[X|Y=y] = \sum_x x \cdot \mathrm{P}(X=x|Y=y).](http://upload.wikimedia.org/math/7/a/3/7a30f7bdaba3178e4cd7aa21a34c771e.png)
![\begin{matrix} \mathrm{E} \left( \mathrm{E}[X|Y] \right) & = & \sum_y \mathrm{E}[X|Y=y] \cdot \mathrm{P}(Y=y) \\ & = & \sum_y \left( \sum_x x \cdot \mathrm{P}(X=x|Y=y) \right) \cdot \mathrm{P}(Y=y) \\ & = & \sum_y \sum_x x \cdot \mathrm{P}(X=x|Y=y) \cdot \mathrm{P}(Y=y) \\ & = & \sum_y \sum_x x \cdot \mathrm{P}(Y=y|X=x) \cdot \mathrm{P}(X=x) \\ & = & \sum_x x \cdot \mathrm{P}(X=x) \cdot \left( \sum_y \mathrm{P}(Y=y|X=x) \right) \\ & = & \sum_x x \cdot \mathrm{P}(X=x) \\ & = & \mathrm{E}[X]. \end{matrix}](http://upload.wikimedia.org/math/5/a/0/5a090c1d87835b1a0e80b4ec9bdb2c67.png)
![\mathrm{E}[X] = \mathrm{E} \left( \mathrm{E}[X|Y] \right).](http://upload.wikimedia.org/math/a/e/c/aec276817c2ff48c9b835b75d6db342a.png)
![|\mathrm{E}[X]| \leq \mathrm{E}[|X|]](http://upload.wikimedia.org/math/b/b/a/bba3c8b5a3510ac7ea36c6b0e7543e6b.png)
![\mathrm{E}[X^\alpha] = \alpha \int_{0}^{\infty} t^{\alpha -1}\mathrm{P}(X>t) \mathrm d t.](http://upload.wikimedia.org/math/9/0/7/90700b05d13e8c5f9d46cc682c475d5b.png)

![\mathrm{E}[X] = \mathrm{E} \begin{bmatrix} x_{1,1} & x_{1,2} & \cdots & x_{1,n} \\ x_{2,1} & x_{2,2} & \cdots & x_{2,n} \\ \vdots \\ x_{m,1} & x_{m,2} & \cdots & x_{m,n} \end{bmatrix} = \begin{bmatrix} \mathrm{E}(x_{1,1}) & \mathrm{E}(x_{1,2}) & \cdots & \mathrm{E}(x_{1,n}) \\ \mathrm{E}(x_{2,1}) & \mathrm{E}(x_{2,2}) & \cdots & \mathrm{E}(x_{2,n}) \\ \vdots \\ \mathrm{E}(x_{m,1}) & \mathrm{E}(x_{m,2}) & \cdots & \mathrm{E}(x_{m,n}) \end{bmatrix}](http://upload.wikimedia.org/math/3/e/b/3eb0cf40024118d50da1d4fda4e69d95.png)











.jpg)

![Ảnh bìa Facebook Timeline đẹp nhất [P2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiErai1d3SbxIXpZmLVa_Abc1NpkhhVamYwCM4_R6EHETUl4Kh7vkj-9lgKm5h2-zzTEMWuLtneTEaAfrBYqRl6y48k3GrDSiop3gS-WzgR-6Ba6C-H1cI8ILft9lJXjz8mbJ84S8ebnts/s72-c/anh_bia_facebook_kenhdaihoc.com_+(1).jpg)
![Ảnh bìa Facebook Timeline đẹp nhất [P3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhk7EG1TIxlQJctZKcpohjBAwzIcfWDo4Jxg6X5DRAk8Ay3dIMI3tC_cvNUYd2-N4ePZzwRTkhkVDHpqlUuKGg991WQhb-eB-JhQGHR9ykJimWATHoujI_8ihMpVh7kdOdDrmbukIsSwJw/s72-c/anh-bia_facebook_kenhdaihoc.com_dep+(1).jpg)
![Ảnh bìa Facebook Timeline đẹp nhất [P4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhS8ADsEtX4FJeXVlCRlZ7iwzWshDFIudf2Mhvo4kDwyOlmse-R1tARAQbs6ZhsHzcThgZF0jm1h72isInAJU1naU8EzGYD10EFDANjy47pG4ptuI__tQ6MrGUmZW251zr8dSZhEhtwJ4s/s72-c/anh_bia_facebook_kenhdaihoc.com_hot+(1).jpg)
.jpg)

.jpg)
0 nhận xét