[HHKG] Quan hệ vuông học {khoảng cách} [lần 1]

 [CHỈ LÀ GỢI Ý ĐỂ BẠN RÈN LUYỆN]

Bài 1:  Cho hình chóp $S.ABCD$, $ABCD$ là hình thoi tâm $O$, $SO\perp (ABCD)$, $AC=4$, $BD=2$, $SO=\sqrt{3}$, $M$ là trung điểm $SC$. Tính khoảng cách giữa hai đường thẳng $SA$ và $BM$.

Hướng dẫn:

Cách 1:

Ta có $SA//OM\Rightarrow SA//(BMD)\Rightarrow d_{SA/BM}=d_{SA/(BMD)}=d_{A/(BMD)}=d_{C/(BMD)}=2d_{H/(BMD)}$

Trong đó $MH\bot AC$ ($H$ là trung điểm của $CO$)
Để tính $d_{H/(BMD)}$ ta cần chú ý: $HO\bot DB$ ta chỉ cần kẻ $HK\bot MO\Rightarrow HK\bot (BMD)\Rightarrow d_{H/(BMD)}=HK=\dfrac{HO.HM}{\sqrt{HO^2+HM^2}}$

Cách 2: 

Dựng đường vuông góc chung

Ta có $SA//OM\Rightarrow SA//(BMD)$ dễ dàng nhận thấy $OM$ là hình chiếu vuông góc của $SA$ trên $(BMD)$
Dựng $ON$ vuông góc với $SA$ thì suy ra $ON\bot (BMD)\Rightarrow ON\bot BM$. Từ $M$ kẻ $MP//ON$ thì $MP$ là đoạn vuông góc chung của $SA$ và $BM$.

Bài 2:Cho hình chóp $S.ABCD$ có đáy $ABCD$ là nửa lục giác đều nội tiếp đường tròn đường kính $AD=2a$, $SA\perp (ABCD)$, $SA=a\sqrt{6}$. Tính $d(AD,(SBC))$

Gợi ý

Nhìn trên hình vẽ ta có : $AD//(SBC)$ nên $d_{AD,(SBC)}$ là độ dài đoạn $BH\perp AD$.

 

Bài 3: Cho tứ diện $SABC$ có đáy là tam giác vuông tại $B$, $BA=BC=a\sqrt{5}$ và khoảng cách từ $A$ tới mặt phẳng $(SBC)$ là $a\sqrt{3}$. Các mặt bên $SAB, SCB$ là các tam giác vuông tại $A, C$. Tính thể tích tứ diện

Hướng dẫn

Dựng CD song song với AB sao cho ABCD la hình vuông. Từ giả thiết suy ra SD vuông góc với mặt phẳng ABCD.

Khoảng cách từ A đến mp(SBC) bằng khoảng cách từ D đến mp(SBC). Gọi K là hình chiếu của D trên SC suy ra DK là khoảng cách từ D đến mp(SBC).
Áp dụng định lí trong tam giác vuông SDC ta có $\frac{1}{DK^2}= \frac{1}{SD^2}+ \frac{1}{DC^2}.$ Từ đó suy ra chiều cao SD của khối chóp.

Gợi ý:

Cách 1: (Hình vẽ 1)
$\bullet$ Gọi $M$ là trung điểm của $BC$ thì $SM, \ AM\bot BC\Rightarrow \widehat{SMA}=60^0$
Gọi $H$ là chân đường cao hạ từ $S$ lên $(ABC)$ thì $H\in AM$
Ta có tam giác $AMS$ đều cạnh bằng $\dfrac{a\sqrt{3}}{2}$ nên $H$ là trung điểm của $AM$
Vì $BC=2MC \Rightarrow d_{B/(SAC)}=2d_{M/(SAC)}$. Mặt khác ta lại có $MA=2HA\Rightarrow d_{M/(SAC)}=2d_{H/(SAC)} \Rightarrow d_{B/(SAC)}=4d_{H/(SAC)}$
$\bullet$Tính $d_{H/(SAC)}$
Kẻ $HE\bot AC,  \ HF\bot SE\Rightarrow HF\bot(SAC)\Rightarrow d_{H/(SAC)}=HF$
Trong tam giác vuông $SHE$ ta có: $\ \dfrac{1}{HF^2}=\dfrac{1}{HE^2}+\dfrac{1}{SH^2} \Rightarrow HF=\dfrac{HE.HS}{\sqrt{HE^2+HS^2}}$
Tính được: $\ HE=AH. \sin 30 = \dfrac{a\sqrt{3}}{8}; SH=\dfrac{3a}{4}$ suy ra $HF=\dfrac{3\sqrt{13}a}{52}$
Vậy $d_{B/(SAC)}=\dfrac{3\sqrt{13}a}{13}$

Cách 2: (Hình vẽ 2)[/B]. Tính trực tiếp đường cao $BK$

Hạ $BK\bot (SAC)$ thì $\triangle{BKA}=\triangle{BKS}=\triangle{BKC} \Rightarrow KA=KC=KS$. Suy ra $H$ là tâm vòng tròn ngoại tiếp tam giác $SAC$.
Áp dụng công thức: $R=\dfrac{abc}{4S} \Rightarrow KC=\dfrac{SA.SC.AC}{4S_{\triangle{SAC}}}=\dfrac{ \dfrac{a^2\sqrt{3}}{2}}{4. \dfrac{a^2\sqrt{39}}{16}}=\dfrac{2\sqrt{13}a}{13}$
Từ đó suy ra $BK=\sqrt{BC^2-KC^2}=\sqrt{a^2-\dfrac{4}{13}a^2}=\dfrac{3\sqrt{13}a}{13}$

Còn 1 trường hợp ( bạn tự giải)
 Bài toán này còn trường hợp điểm $H$ nằm ngoài tam giác $ABC$

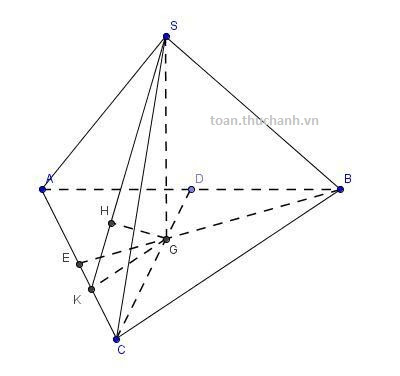
Bài 4: Cho hình chóp $S.ABC,$ với đáy $ABC$ là tam giác vuông cân tại $C,$ độ dài cạnh huyền trong tam giác này bằng $3a.$ Gọi $G$ là trọng tâm của tam giác $ABC.$ Biết rằng $SG \perp (ABC)$ và $SB=\dfrac{a\sqrt{14}}{2}.$ Tính khoảng cách từ $B$ đến mặt phẳng $(SAC).$

Gợi ý cách làm bằng hình vẽ

+) Để tính khoảng cách từ B tới mặt phẳng $(SAC)$ ta sẽ đi tính $d(G;(SAC))$sau đó suy ra khoảng cách từ B tới $(SAC)$
+) Kẻ $GK\bot AC$và $GH\bot SK$
+) $d(G;(SAC)) =GH$
+) $d(B;(SAC))=\dfrac{3}{2}d(G;(SAC))$

Bài 5: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$. $mp(SAB) \bot (ABCD)$Có $SA=SB$, góc tạo bởi $\ SC$ và mặt đáy bằng $45^0$. Gọi $\ E$ là trung điểm của $\ AB$. Tính Khoảng cách giữa $\ SD$ và $\ EC$

Hướng dẫn
Về cách xác định khoảng cách giữa 2 đường thẳng chéo nhau thì không thì cứ tuân theo lý thuyết
+) Xác định độ dài đoạn vuông góc chung, Cái này ít gặp trong giải toán vì xác định thường khó và phức tạp
+) Vận dụng tính chất : Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách từ đường thẳng này tới mặt phẳng song song song với nó và chứa đường kia.

Các bạn quan sát hình vẽ sẽ tìm ra lời giải

+) Gọi M là trung điểm của BC. Khi đó ta dẽ dàng chứng mình được $CE \bot DM$ (bài toán này quen thuộc)
+) Khoảng cách là $d(CE;SD)=d(CE;mp(SGD))=EH$

Bài 6: Cho hình chóp $S.ABC$ có $SA \bot (ABC)$ ;$SA=1,$ có đáy là tam giác $ABC$ vuông tại $A.$ Biết $AB=m$ ; $AC=n$ sao cho $m+n=1$ ;  (m  ;  n >0). Tìm một điểm $I$ trong không gian sao cho khoảng cách từ điểm $I$ đến $(SBC)$ luôn không đổi.

Gọi $M,N$ là các điểm thuộc $AB, \ AC$ sao cho $\ AM= AN=AS=1$. Ta dựng hình vuông $\ AMDN$
Khi đó $SB=\sqrt{SA^2+AB^2}=\sqrt{1+AB^2}; \ CD=\sqrt{ND^2+NC^2}=\sqrt{1+NC^2}$
Vì $AB+AC=1; \ AC+NC=1\Rightarrow AB=NC\Rightarrow SB=CD$
Tương tự ta có: $SC=BD$$\Rightarrow \triangle{SBC}=\triangle{DCB}$
Gọi $\ O, \ I$ lần lượt là trung điểm của $AD,  SD$ thì $OI=\dfrac{1}{2} SA=\dfrac{1}{2}$
Mặt khác ta có  $\ V_{SBCI}=V_{DBCI}$ do $\ I$ là trung điểm của $SD$ và có chung đáy $BCI$

Từ đó ta suy ra $d_{I/(SBC)}=d_{I/(BCD)}=\dfrac{1}{2}$
Vậy điểm $I$ cần tìm là trung điểm của đoạn $SD$